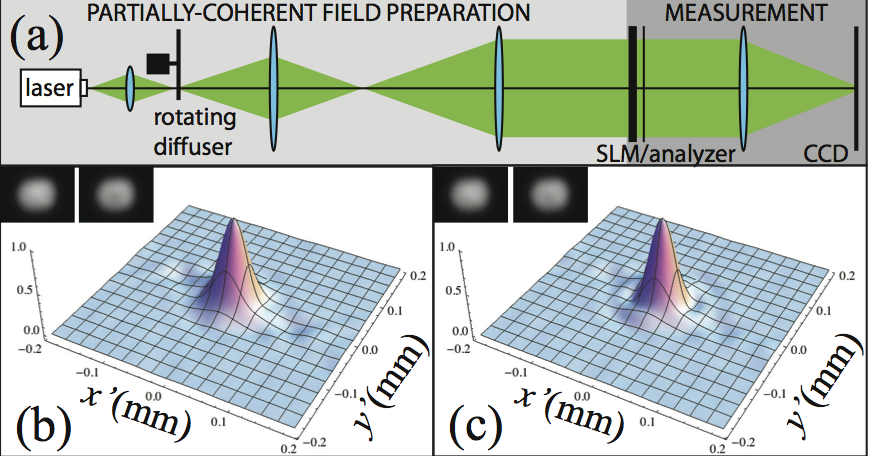
Recent work in our group has focused on simple methods for measuring spatial coherence that do not require wavefront division. In particular, we recently proposed an approach where an obstacle is inserted at the test plane, and the difference of irradiance measurements with and without this obstacle gives access to the spatial coherence at all pairs of points whose centroid is the obstacle’s centroid. Our group has also published theoretical work on the propagation of partially coherent fields. (See also section on Wigner functions.)
Simple non-interferometric methods for the measurement of spatial coherence
Journal articles
- S.A. Wadood, K. Liang, Y. Zhou, J. Yang, M.A. Alonso, X.F. Qian, T. Malhotra, S.M. Hashemi Rafsanjani, A.N. Jordan, R.W. Boyd, and N.A. Vamivakas, “Experimental demonstration of superresolution of partially coherent light sources using parity sorting,” Opt. Express 29, 22034-22043 (2021).
- K.A. Sharma, G. Costello, E. Vélez-Juárez, T.G. Brown, and M.A. Alonso, “Measuring vector field correlations using diffraction,” Opt. Express 26, 8301-8313 (2018).
- K.A. Sharma, T.G. Brown, and M.A. Alonso, “Phase-space approach to lensless measurements of optical field correlations,” Opt. Express 24, 16099-16110 (2016).
- J.K. Wood, K.A. Sharma, S. Cho, T.G. Brown, and M.A. Alonso, “Using shadows for measuring spatial coherence,” Opt. Lett. 39, 4927-4930 (2014).
- S. Cho, M.A. Alonso, and T.G. Brown, “Measurement of spatial coherence through diffraction from a transparent mask with a phase discontinuity” Opt. Lett. 37, 2724-2726 (2012).
- S. Cho and M.A. Alonso, “Ambiguity function and phase space tomography for nonparaxial fields,” J. Opt. Soc. Am. A 28, 897-902 (2011).
Conference proceedings
Mathematical descriptions of the propagation of spatial coherence
Journal articles
- M. Marasinghe, M. Premaratne, D. Paganin, and M.A. Alonso, “Coherence vortices in Mie scattered partially coherent fields,” Opt. Express 20, 2858-2875 (2012).
- J.C. Petruccelli, N.J. Moore, and M.A. Alonso, “Two methods for modeling the propagation of the coherence and polarization properties of nonparaxial fields,” Opt. Commun. 283, 4457-4466 (2010).
- J.C. Petruccelli and M.A. Alonso, “Propagation of nonparaxial partially coherent fields across interfaces using generalized radiometry,” J. Opt. Soc. Am. A 26, 2012-2022 (2009).
- M.A. Alonso and E. Wolf, “The cross-spectral density matrix of a planar, electromagnetic stochastic source as a correlation matrix,” Opt. Commun. 281, 2393-2396 (2008).
- J.C. Petruccelli and M.A. Alonso, “Ray-based propagation of the cross-spectral density,” J. Opt. Soc. Am. A 25, 1395-1405 (2008).
- J.C. Petruccelli and M.A. Alonso, “Propagation of partially coherent fields through planar dielectric boundaries using angle-impact Wigner functions I. Two dimensions,” J. Opt. Soc. Am. A 24, 2590-2603 (2007).
- M.A. Alonso, O. Korotkova, and E. Wolf, “Propagation of the electric correlation matrix and the van Cittert-Zernike theorem for random electromagnetic fields,” J. Mod. Opt. 53, 969-978 (2006).