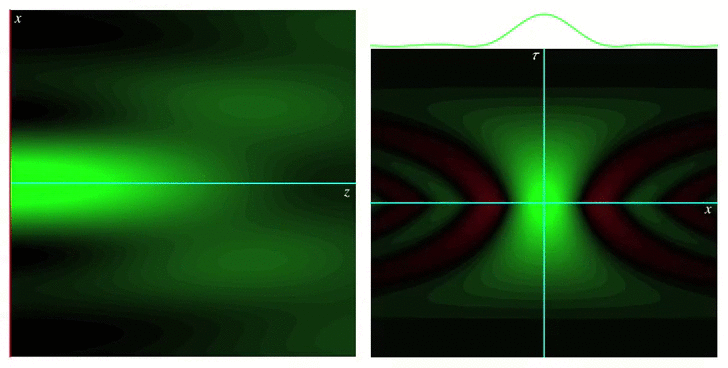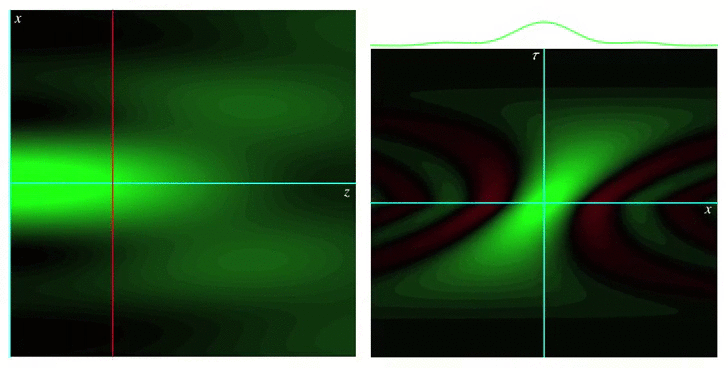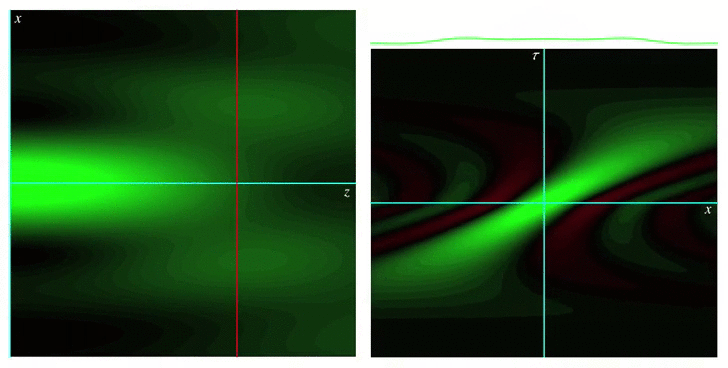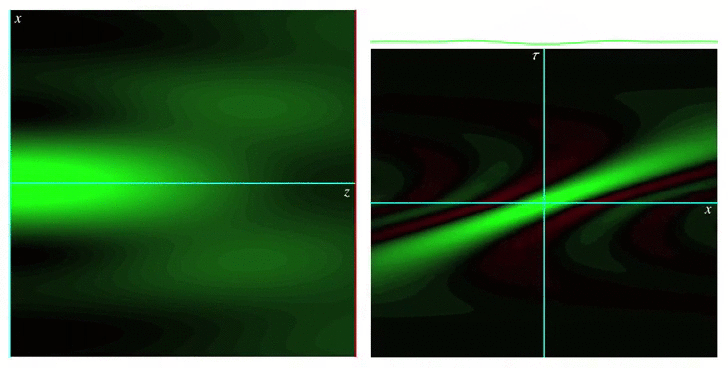
The Wigner function or Wigner distribution is a bilinear integral transformation that allows representing a function jointly in terms of its original variable and its Fourier conjugate. For example, by using the Wigner function, a time signal representing a piece of music can be represented jointly in terms of time and frequency, providing a representation qualitatively similar to a musical score. Wigner functions were first defined by Eugene Wigner in 1932 to describe the wavefunction of a quantum particle in terms of both position and momentum, hence providing a classical-like picture. They also have been applied to modeling the propagation of optical wave fields in terms of rays, and also for the propagation of optical pulses through simple dispersive media.
Our group’s work on Wigner functions and other phase space representations has included studying their behavior in certain limits, as well as providing new definitions for them that are best suited for describing different physical situations, such as nonparaxial propagation of scalar and electromagnetic fields, diffraction effects, propagation of pulses through transparent media with arbitrary dispersion properties, and wave fields constrained to simple curved spaces.
Review/tutorial articles
- M.A. Alonso, “Wigner functions in optics: describing beams as ray bundles and pulses as particle ensembles,” (review article) Adv. Opt. Phot. 3, 272-365 (2011).
- J.C. Petruccelli and M.A. Alonso, “The Wigner function in optics,” The Optics Encyclopedia (Wiley VCH, 2015).
Standard Wigner functions and their use in optics
Journal articles
- M.A. Alonso and G.W. Forbes, “Phase space distributions for high-frequency fields,” J. Opt. Soc. Am. A 17, 2288-2300 (2000).
- M.A. Alonso, “Diffraction of paraxial partially coherent fields by planar obstacles in the Wigner representation,” J. Opt. Soc. Am. A 26, 1588-1597 (2009).
Wigner functions and other phase distributions for nonparaxial scalar and electromagnetic wave fields
Journal articles
- J.C. Petruccelli and M.A. Alonso, “A generalized radiance model for the propagation of light within anisotropic media,” J. Opt. Soc. Am. A 28, 791-800 (2011).
- J.C. Petruccelli and M.A. Alonso, “Propagation of nonparaxial partially coherent fields across interfaces using generalized radiometry,” J. Opt. Soc. Am. A 26, 2012-2022 (2009).
- S. Cho, J.C. Petruccelli and M.A. Alonso, “Wigner functions for paraxial and nonparaxial fields,” J. Mod. Opt. 56, 1843-1852 (2009).
- J.C. Petruccelli and M.A. Alonso, “Ray-based propagation of the cross-spectral density,” J. Opt. Soc. Am. A 25, 1395-1405 (2008).
- J.C. Petruccelli and M.A. Alonso, “Propagation of partially coherent fields through planar dielectric boundaries using angle-impact Wigner functions I. Two dimensions,” J. Opt. Soc. Am. A 24, 2590-2603 (2007).
- M.A. Alonso, “Wigner functions for nonparaxial, arbitrarily polarized electromagnetic wave fields in free space,” J. Opt. Soc. Am. A 21, 2233-2243 (2004).
- M.A. Alonso and A. Antillon, “Angle-impact representations for wave fields in convex cavities,” Opt. Commun. 224, 159-173 (2003).
- M.A. Alonso, “Exact description of free electromagnetic wave fields in terms of rays,” Opt. Exp. 11, 3128-3135 (2003).
- L.E. Vicent and M.A. Alonso, “Generalized radiometry as a tool for the propagation of partially coherent fields,” Opt. Commun. 207, 101-112 (2002).
- M.A. Alonso, “Radiometry and wide-angle wave fields. III. Partial coherence,” J. Opt. Soc. Am. A 18, 2502-2511 (2001).
- M.A. Alonso, “Radiometry and wide-angle wave fields. II. Coherent fields in three dimensions,” J. Opt. Soc. Am. A 18, 910-918 (2001).
- M.A. Alonso, “Radiometry and wide-angle wave fields. I. Coherent fields in two dimensions,” J. Opt. Soc. Am. A 18, 902-909 (2001).
- K.B. Wolf, M.A. Alonso, and G.W. Forbes, “Wigner functions for Helmholtz wave fields,” J. Opt. Soc. Am. A 16, 2476-2487 (1999).
Conference proceedings
- M.A. Alonso, S. Cho and T.G. Brown, “Simple methods for measuring spatial coherence and their relation to the Wigner function,” IEEE Proceedings of the 11th Euro-American Workshop on Information Optics, 1-3 (2012).
- M.A. Alonso, J.C. Petruccelli, and S. Cho, “Generalized phase space representations in classical optics,” 22nd Congress of the International Commission for Optics: Light for the Development of the World, SPIE Proceedings 8011, 80116E (2011).
- J.C. Petruccelli and M.A. Alonso, “Propagation of Partially Coherent, Partially Polarized Fields via a Wigner Representation in Direction and Angular Momentum,” in Conference on Coherence in Quantum Optics, OSA Technical Digest (CD) (Optical Society of America, 2007), paper CSuA46.
- M.A. Alonso, “Wigner functions for nonparaxial classical optical fields,” Proceedings of the XXV International Colloquium on Group theoretical Methods in Physics, G. S. Pogosyan, L. E. Vicent, and K. B. Wolf, Eds. Institute of Physics Conference Series 185 (2005), pp. 29-36.
- M.A. Alonso, “Exact description of electromagnetic waves in terms of rays,” 2004 URSI EMTS International Symposium on Electromagnetic Theory Proceedings (Edizioni Plus, Pisa 2004), pp. 242-244.
Highlights
Wigner functions for short pulses in media with arbitrary dispersion
Journal articles
Wigner functions for curved spaces
Journal articles