Full Poincaré Fields Composed of a Discrete Number of Plane Waves

Author

Lingyi Cai

Mentor

Miguel Alonso

Abstract

In recent years, full Poincaré (FP) fields have attracted an increasing amount of interest. Conventionally, the FP fields are composed of beams with Gaussian modes and Laguerre-Gaussian modes. In this thesis, we numerically and analytically analyzed the superposition of multiple paraxial plane waves and discovered the pattern of such superpositions composing FP fields. MATLAB scripts are used to simulate both the transverse plane distribution and the polarization states in the Poincaré sphere. We found that three waves are sufficient to compose a FP field, and from the FP configurations, we proposed a hypothesis of the requirements to compose FP fields with only three plane waves.

Background

The polarization of electromagnetic waves is defined as the statistical description of the geometric behavior of the oscillations of the field vector. In isotropic media, the oscillation of the field is always perpendicular to the direction of the propagation of the wave. When multiple coherent waves are propagating in directions with a slight difference, the longitudinal polarization component will be ignorable and the polarization distribution over the transverse plane will be nonuniform.

Poincaré sphere

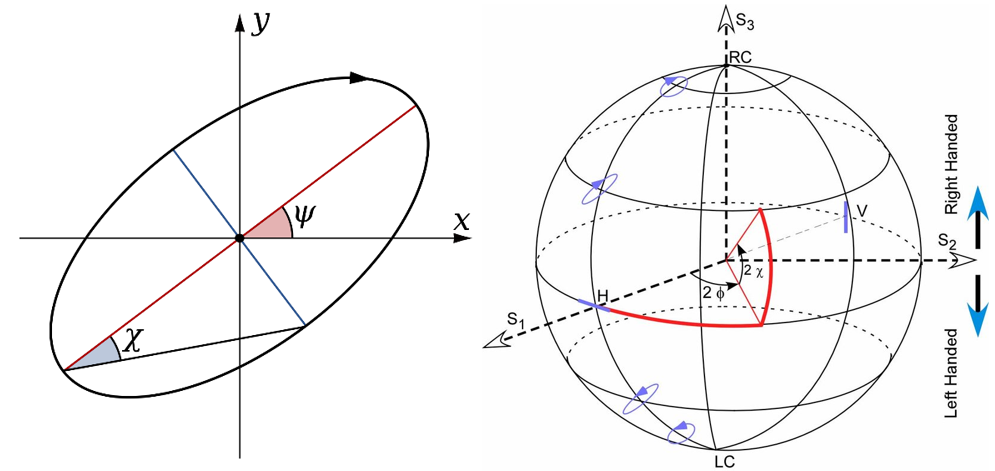
In 1852, George Gabriel Stokes introduced the Stokes parameters which describe the polarization with the total intensity I, the fractional degree of polarization p, and the shape parameters of the polarization ellipse. Divide the parameters by the intensity gives the normalized Stokes vector s_2D=(s₁,s₂,s₃). When s₁, s₂, and s₃ are used as a basis of coordinate, every polarization state represented by the normalized Stokes parameters will correspond to a single point interior of a unit sphere centered at the origin, which is called the Poincaré sphere.

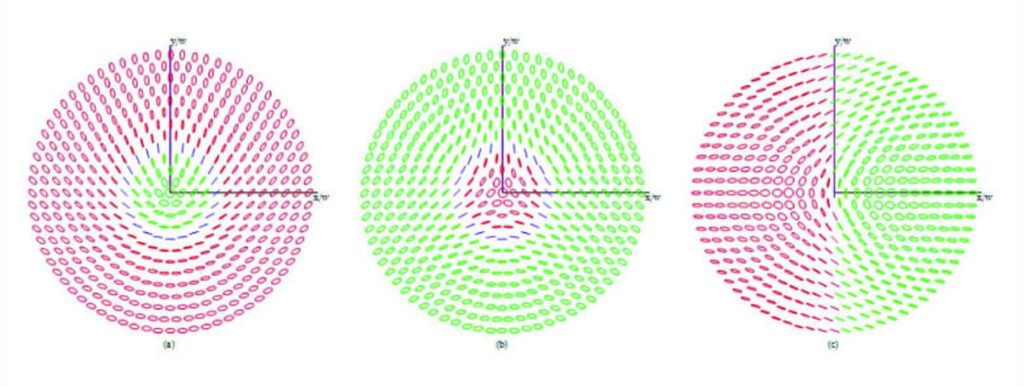
Full Poincaré Field

Full Poincaré fields are fields with nonuniform polarization distribution which spans the entire surface when projected onto the Poincaré sphere. Amber M. Beckley, et al. (2010) first introduced that the beams can be constructed from a coaxial superposition of a fundamental Gaussian mode and a spiral-phase Laguerre-Gauss mode having orthogonal polarizations. Our goal in this thesis is to use plane waves instead to compose Full Poincaré fields.

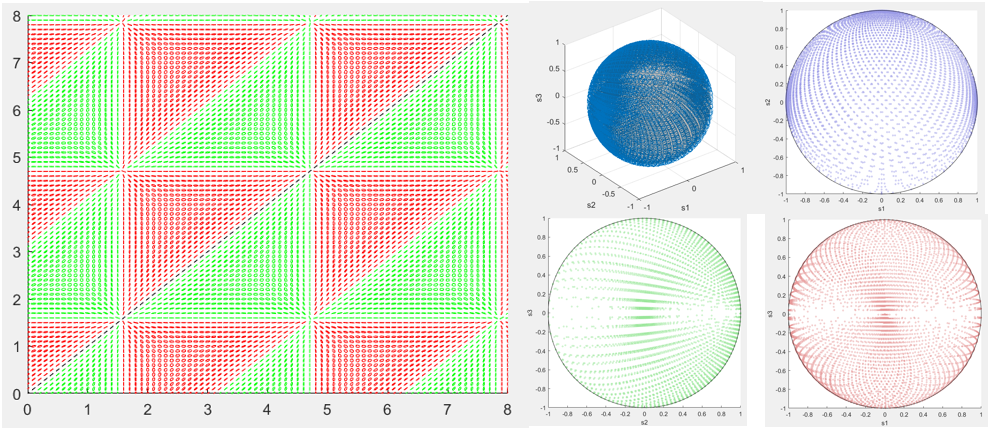
Results

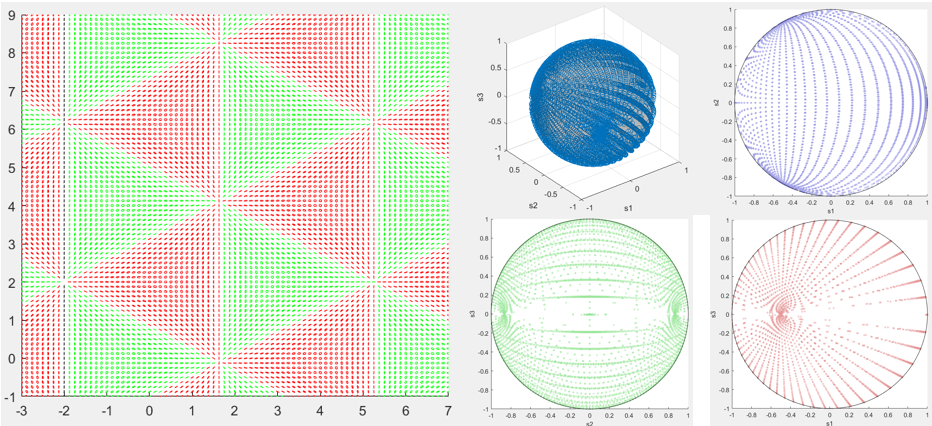
Hypothesis

Requirement for Composing FP Fields with Three Plane Waves:

For three fully polarized plane waves E₁,E₂,E₃, exist E₁, such that:

(1)k₂+k₃=mk₁, where m∈R;

(2)e₁=±(e₂+e₃);

(3)(k₁^T∙e₂ )(k₁^T∙e₃ )<0