
Team
- Naman Bharara
- Andrew Dettor
- Julie Fleischman
- Huilin Piao
Mentor
Fritz Ebner
Abstract
Pickleball is new to the sports analytics industry, as it has only recently been rising in popularity. Our project is to aid in the development of a pickleball analytics platform by improving ball detection and tracking. The baseline was a TrackNetV2 (Sun et. al. 2020) model trained on badminton, and the purpose of this project is to improve the model using transfer learning techniques to improve its performance in pickleball.
Introduction
Our team developed an adaptation for a ball detection program for use in pickleball analytics. We utilize transfer learning techniques to develop a better ball tracking solution. An existing object tracking system known as Tracknet 2.0 was developed in Taiwan, by a team of researchers working on making a shuttle tracking program for badminton. This model was trained on over 55,000 frames of professional badminton matches, and our project was to take this pre-trained model and adapt it to pickleball.
Dataset
Raw Data
The dataset developed for this analysis was based on a fifty-four-minutes recording of a Pro Senior Mixed Doubles Gold Medal Match in September, 2021. The dimension of the video is 1920 x 1080, and the video was recorded at a 60 frames per second rate.
Preprocessing
To avoid overfitting and reduce dataset size, we screen out unrelated frames and segments for game related clips by trimming videos to moments starting from ball serving to score. A seven-minute video with 12810 frames in total is trimmed with recording all the complete plays.
We then utilize a labeling tool in Python provided by the authors of TrackNetV2 to label the ball status for the first 12,000 frames of the play. Each frame attaches the following attributes: “Frame”, “Visibility”, “X”, “Y”. Frame records the number of frames. Visibility is a dummy variable indicating whether the ball is visible in the frame. Visibility = 0 implies that the ball is not within the frame. “X” and “Y” present the x and y coordinates of the detected ball in pixels. Coordinates for balls with visibility = 0 are marked as (-1, -1).
Hypothesis
We hypothesize that using transfer learning techniques, we can achieve a true positive rate of 65% for pickleball ball detection. The true positive rate, which is the percentage of balls that are correctly recognized and labeled by the model, is used as the basis for developing a quantified goal. This is because the ball detection model is going to be implemented in a more expansive piece of software for analyzing pickleball playing, and therefore it is more important to capture a high percentage of balls when they are visible than overall accuracy, which includes both correctly capturing balls when they are visible and not predicting locations when the ball is not visible.
Model Development
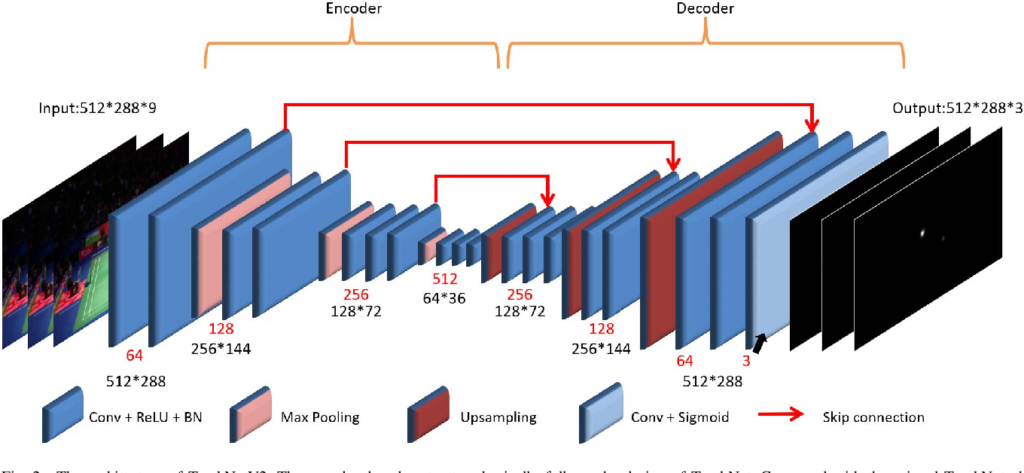
The model being used in this analysis is TrackNetV2. This was developed by researchers from Taiwan National Chiao Tung University (Sun et. al. 2020) for badminton. The TrackNetV2 model is a 63 layer encoder-decoder neural network. It contains 18 convolutional layers. In aggregate, this corresponds to 11,334,531 trainable parameters and 8,064 non-trainable parameters. An encoder-decoder model is a neural network which scales down dimensionality in the first half of the model through an encoding process, and then uses a decoding process to scale it back to the input frame size.
Baseline Performance
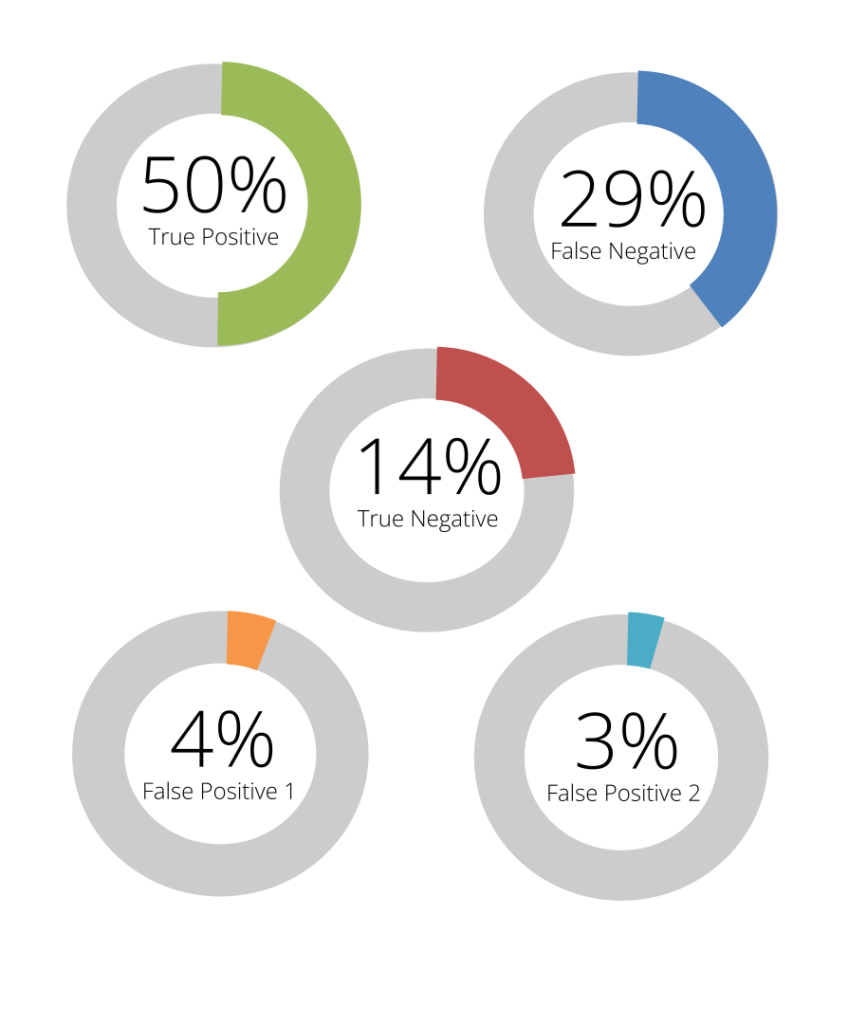
Assessing the differences between the beginning model weights as trained on badminton in a pickleball context and comparing to hand-labelled data, the baseline performance of the model weights follows.
Transfer Learning
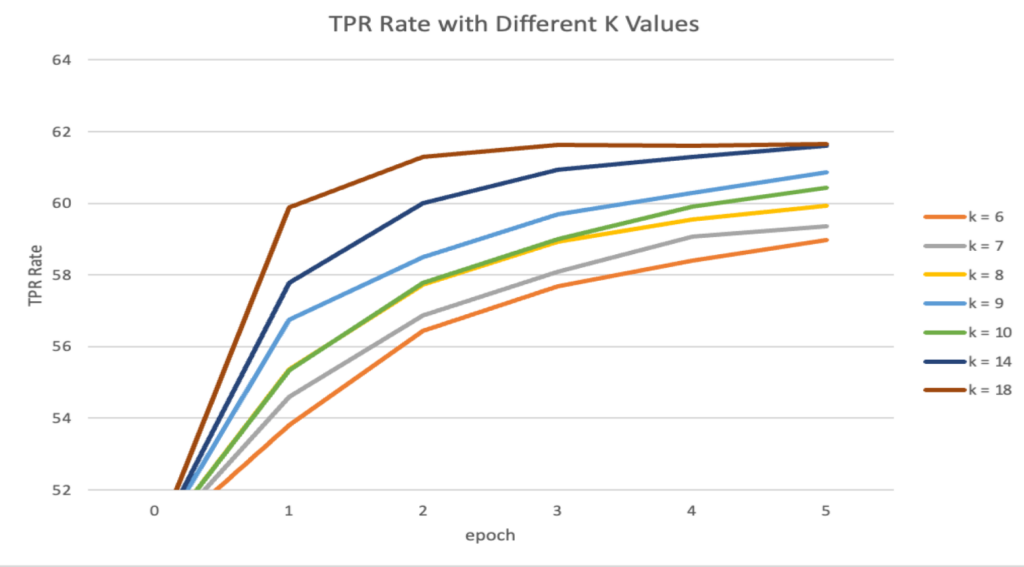
The approach utilized here is to freeze training of early layers in the network and only adjust a fixed number of final layers of the network. Since early layers learn lower-level features, and pickleball low-level features are similar to badminton low-level features, there is no need to adjust weights from those early layers. The goal with layer freezing is to find optimal hyperparameters, including the number of epochs, learning rate, and number of convolutional layers to improve starting from the end of the network, which were optimized in that order. Results from the below figure indicate that TPR converges to the same value when any more than 14 layers are unfrozen, so this is the number that the final transfer learning process iterates through.
Results
Results show that training on 20 epochs yields a 12% increase in TPR, which is close to the goal of 65% TPR in total.
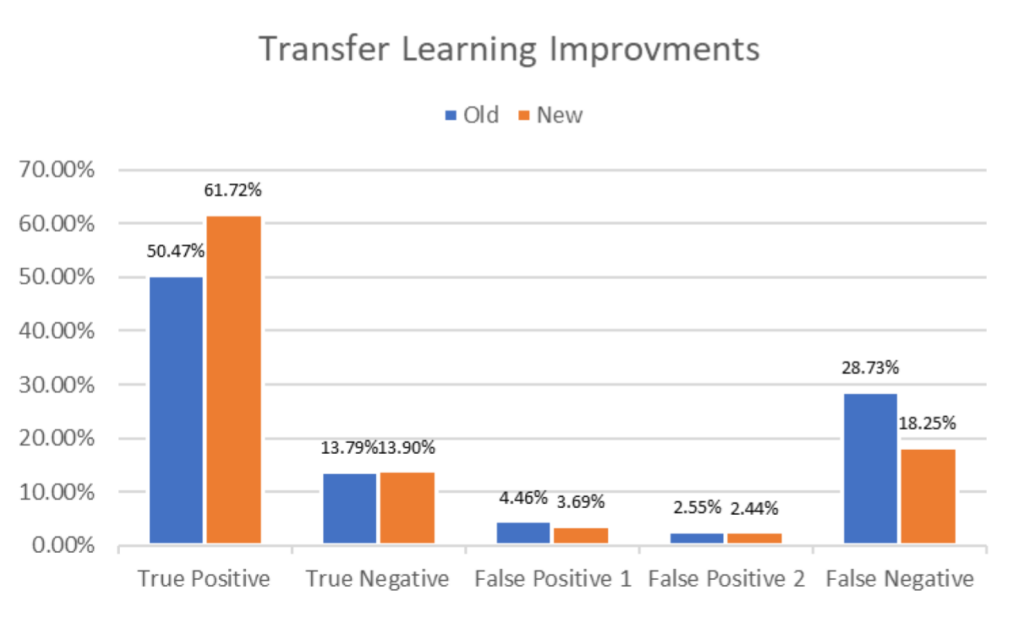
The other notable finding is that true negatives and false positives all remain relatively consistent, which means that the main change from the original model to the new model are between false negatives and true positives. Since false negatives are frames where there is a ball in the screen according to ground truth but the model is not making a prediction, this means that the additional training helped the model to better recognize the pickleball.
Further research should investigate the results of running this transfer learning on more epochs, and test if there are marginal benefits from longer and more learning iterations.
